Tração é toda força com intuito de puxar ou empurrar um corpo. Quando puxamos um carro amarrado a uma corda, estamos realizando uma força de tração na corda, que por sua vez transmite essa força para o carro, e faz com que ele se mova. Quando dizemos que o carro tem tração em duas rodas ou nas quatro rodas, significa que todas essas rodas fazem com que o carro se movimente.
Melhores alunos para o melhor da Física

Galileu Galilei
sexta-feira, 22 de junho de 2012
Planos Inclinados
São superfícies planas, rígidas, inclinadas em relação à horizontal, que servem para multiplicar forças, constituindo, portanto, máquinas simples.
Tábuas que se apóiam no solo por uma de suas extremidades e num caminhão pela outra, sobre a qual operários empurram 'cargas', são exemplos de planos inclinados. Rampas de acesso a morros ou construções elevadas são também, planos inclinados. Eles comparecem, como veremos adiante, em facas, cunhas, talhadeiras, machados, parafusos, porcas, roscas-sem-fim, prensas, escadas rolantes etc.
http://www.feiradeciencias.com.br/sala06/06_RE04.asp
São superfícies planas, rígidas, inclinadas em relação à horizontal, que servem para multiplicar forças, constituindo, portanto, máquinas simples.
Tábuas que se apóiam no solo por uma de suas extremidades e num caminhão pela outra, sobre a qual operários empurram 'cargas', são exemplos de planos inclinados. Rampas de acesso a morros ou construções elevadas são também, planos inclinados. Eles comparecem, como veremos adiante, em facas, cunhas, talhadeiras, machados, parafusos, porcas, roscas-sem-fim, prensas, escadas rolantes etc.
 |
Daniel Morozeski
Plano Inclinado
Quando um objeto se encontra sobre um plano inclinado, sofre a ação de uma força de reação normal ao apoio, conforme figura 01.
Neste caso foi desprezada a força de atrito. A força peso age na vertical, dirigida para o centro da Terra (de cima para baixo). Fixemos um plano cartesiano de coordenadas com o eixo x paralelo ao plano inclinado e o eixo y apontando para a direção da força normal, perpendicular a este plano. A força resultante na direção x é Px e pode ser escrita em função do ângulo θ. Então se obtém:
Px = P.senθ
A força normal tem o mesmo módulo de Py:
N = Py
Se
Py = P.cosθ
Então
N = P.cosθ
Ou seja, neste sistema de referência adotado, a força peso é representada por duas componentes, Px na direção x ou horizontal e Py na direção y ou vertical.
Fica evidente que quando o ângulo de inclinação do plano em relação à horizontal for maior, maior será a intensidade da componente da força peso na direção x, e menor será a intensidade da componente da força atuante na direção y, até um limite máximo, onde o ângulo for de 90º. Neste caso, a componente Px é igual ao peso P e a componente Py vale 0. Isso pode ser demonstrado:
Para a componente x:
Px = P.sen90º
Logo
Px = P.1
Pois
sen90º = 1
E obtemos:
Py = P
Para a componente y:
Py = P.cos90º
Logo,
Py = 0
Pois
cos90º = 0
Giovana e Laila
Consideremos que uma pessoa de massa m e peso 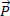
esteja sobre uma balança (modelo usado em farmácias) colocada no interior de um elevador, como mostra a figura acima. Suponhamos então que o mostrador da balança nos mostre os valores em unidades de força.
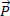
Sabemos que a pessoa sobre o prato da balança aplica uma força 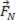 e, de acordo com a Lei da Ação e Reação, o prato da balança exerce sobre a pessoa uma força de mesma intensidade, porém de sentido contrário, portanto a força é -
e, de acordo com a Lei da Ação e Reação, o prato da balança exerce sobre a pessoa uma força de mesma intensidade, porém de sentido contrário, portanto a força é - 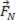 . Não podemos nos esquecer de que ainda sobre a pessoa está atuando a força peso
. Não podemos nos esquecer de que ainda sobre a pessoa está atuando a força peso 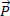 .
.
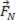 e, de acordo com a Lei da Ação e Reação, o prato da balança exerce sobre a pessoa uma força de mesma intensidade, porém de sentido contrário, portanto a força é -
e, de acordo com a Lei da Ação e Reação, o prato da balança exerce sobre a pessoa uma força de mesma intensidade, porém de sentido contrário, portanto a força é - 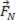 . Não podemos nos esquecer de que ainda sobre a pessoa está atuando a força peso
. Não podemos nos esquecer de que ainda sobre a pessoa está atuando a força peso 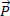 .
.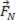 . Caso o elevador esteja em repouso ou movendo-se verticalmente com velocidade constante (subindo ou descendo), a resultante das forças sobre o indivíduo é nula
. Caso o elevador esteja em repouso ou movendo-se verticalmente com velocidade constante (subindo ou descendo), a resultante das forças sobre o indivíduo é nula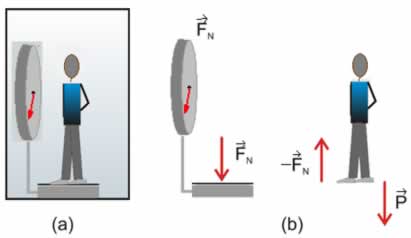
http://www.mundoeducacao.com.br/fisica/elevadores-movimento-vertical.htm
Daniel Morozeski
Força Normal
A
força normal é a reação perpendicular do plano de apoio sobre o plano inferior
do corpo. Embora costume ser representada por uma seta única, na verdade ela se
difunde por toda a superfície de contato.
Plano inclinado
O plano inclinado é um exemplo de máquina simples. Como o nome sugere, trata-se de uma superfície plana cujos pontos de início e fim estão a alturas diferentes.
Ao mover um objeto sobre um plano inclinado em vez de movê-lo sobre um plano completamente vertical, o total de força F a ser aplicada é reduzido, ao custo de um aumento na distância pela qual o objeto tem de ser deslocado.
Observe que pela Lei da Conservação de Energia, a mesma quantidade de energia mecânica é requerida para levantar um dado objeto até uma certa altura, seja através do plano inclinado ou do plano vertical. No entanto, o plano inclinado permite que o mesmo trabalho seja realizado aplicando-se uma força menor por uma distância maior.
Resumindo, o plano inclinado permite uma troca força x distância que é conveniente nas suas aplicações.
Plano Inclinado
Dadas duas trajetórias:
Em qual delas é "mais fácil" carregar o bloco?
Obviamente, na trajetória inclinada, pois no primeiro caso, teremos que realizar uma força que seja maior que o peso do corpo. Já no segundo caso, Defermos fazer uma força que seja maior que uma das componentes de seu peso, neste caso, a componete horizontal, que terá instensidade menor conforme o ângulo formado for menor.
Por isso, no nosso cotidiano, usamos muito o plano inclinado para facilitar certas tarefas.
Ao analizarmos as forças que atuam sobre um corpo em um plano inclinado, temos:
A força Peso e a força Normal, neste caso, não tem o mesma direção pois, como já vimos, a força Peso, é causada pela aceleração da gravidade, que tem origem no centro da Terra, logo a força Peso têm sempre direção vertical. Já a força Normal é a força de reação, e têm origem na superfície onde o movimento ocorre, logo tem um ângulo igual ao plano do movimento.
Para que seja possível realizar este cálculo devemos estabelecer algumas relações:
- Podemos definir o plano cartesiano com inclinação igual ao plano inclinado, ou seja, com o eixo x formando um ângulo igual ao do plano, e o eixo y, perpendicular ao eixo x;
- A força Normal será igual à decomposição da força Peso no eixo y;
- A decomposição da força Peso no eixo x será a responsável pelo deslocamento do bloco;
- O ângulo formado entre a força Peso e a sua decomposição no eixo y, será igual ao ângulo formado entre o plano e a horizontal;
- Se houver força de atrito, esta se oporá ao movimento, neste caso, apontará para cima.
Sabendo isto podemos dividir as resultantes da força em cada direção:
Em y:
como o bloco não se desloca para baixo e nem para cima, esta resultante é nula, então:
mas
então:
Em x:
mas
então:
Exemplo:
Um corpo de massa 12kg é abandonado sobre um plano inclinado formando 30° com a horizontal. O coeficiente de atrito dinâmico entre o bloco e o plano é 0,2. Qual é a aceleração do bloco?
Em y:
Em x:
Elevadores
Nossa força peso (P = m.g), sempre apontando para baixo, cria uma força normal de reação (FN) sempre perpendicular à superfície de contato, geralmente aplicada em nossos pés, e, neste caso, apontando para cima.
Quando entramos em um elevador, de acordo com o seu movimento podemos sentir diferentes sensações. Lembrando que de acordo com a 1ª Lei de Newton, o corpo, por inércia, tende a manter seu estado, seja ele de repouso ou de MRU. E de acordo com o princípio fundamental da Dinâmica, a força resultante (FR) pode ser calculada por FR = m.a, onde m é a massa do corpo e a é a aceleração desenvolvida pelo mesmo.
Há cinco casos possíveis:
- Elevador parado ou subindo e descendo com velocidades constantes (MRU):
Nesses casos, a força normal aplicada em nossos pés é igual à nossa força peso, pois a única aceleração que estamos sentindo é a gravidade. A força resultante entre a normal e a peso é nula. FR = 0 --> FN = P
-Elevador iniciando seu movimento de subida:
Para subir, o elevador faz uma força para cima, tendo uma aceleração positiva voltada para cima. Como a resultante está para cima, a força normal é maior que a força peso. FN > P --> FR = FN - P
-Elevador terminando seu movimento de subida:
Para parar, o elevador desacelera fazendo com que a resultante esteja voltada para baixo, fazendo-o frear. P > FN --> FR = P - FN
-Elevador iniciando o movimento de descida:
Como está descendo de maneira acelerada, sua resultante está voltada para baixo. P > FN --> FR = P - FN
-Elevador terminando o movimento de descida:
Como o elevador está descendo, aplica uma força voltada para cima para parar. FN > P --> FR = FN - P
Como nossa força P é sempre constante, uma balança colocada no piso do elevador indicaria o valor da força FN aplicada em cada caso. Como exemplo, uma pessoa de massa = 60 Kg, em um elevador que sobe e desce com uma aceleração de 3 m/s², tem uma força P = 600 N (considerando g = 10 m/s²) e a balança indicará sua FN variando de 420 N a 780 N. Com isso podemos desmentir a falsa ideia de que a balança mede nossa força peso, ela mede a força normal de reação à peso, que, como vimos, pode variar dependendo da situação.
Uma curiosidade é que se o elevador descer com uma aceleração igual à gravidade (simplesmente cair sob a ação da gravidade), a sua força normal é nula (FN = 0), sendo assim, a pessoa flutuaria dentro do elevador. Este mesmo efeito é utilizado em aviões em queda livre para treinamento de pilotos e astronautas, simulando a falta de gravidade
Há cinco casos possíveis:
- Elevador parado ou subindo e descendo com velocidades constantes (MRU):
Nesses casos, a força normal aplicada em nossos pés é igual à nossa força peso, pois a única aceleração que estamos sentindo é a gravidade. A força resultante entre a normal e a peso é nula. FR = 0 --> FN = P
-Elevador iniciando seu movimento de subida:
Para subir, o elevador faz uma força para cima, tendo uma aceleração positiva voltada para cima. Como a resultante está para cima, a força normal é maior que a força peso. FN > P --> FR = FN - P
-Elevador terminando seu movimento de subida:
Para parar, o elevador desacelera fazendo com que a resultante esteja voltada para baixo, fazendo-o frear. P > FN --> FR = P - FN
-Elevador iniciando o movimento de descida:
Como está descendo de maneira acelerada, sua resultante está voltada para baixo. P > FN --> FR = P - FN
-Elevador terminando o movimento de descida:
Como o elevador está descendo, aplica uma força voltada para cima para parar. FN > P --> FR = FN - P
Como nossa força P é sempre constante, uma balança colocada no piso do elevador indicaria o valor da força FN aplicada em cada caso. Como exemplo, uma pessoa de massa = 60 Kg, em um elevador que sobe e desce com uma aceleração de 3 m/s², tem uma força P = 600 N (considerando g = 10 m/s²) e a balança indicará sua FN variando de 420 N a 780 N. Com isso podemos desmentir a falsa ideia de que a balança mede nossa força peso, ela mede a força normal de reação à peso, que, como vimos, pode variar dependendo da situação.
Uma curiosidade é que se o elevador descer com uma aceleração igual à gravidade (simplesmente cair sob a ação da gravidade), a sua força normal é nula (FN = 0), sendo assim, a pessoa flutuaria dentro do elevador. Este mesmo efeito é utilizado em aviões em queda livre para treinamento de pilotos e astronautas, simulando a falta de gravidade

Segunda lei de newton
Vamos entender melhor a segunda lei de Newton, aplicar a segunda lei e resolver exercícios utilizando este recurso.
Todos os dias observamos vários tipos de movimento. São carros acelerando, objetos caindo, pessoas andando, a todo o momento observamos estes movimentos que se alteram a cada instante. Estas alterações no movimento são determinadas pela força resultante e pela massa dos corpos. A aceleração é o que determina se o carro vai parar ou vai “ganhar” velocidade. A segunda lei de Newton relaciona as grandezas que podem alterar um movimento.
Enunciado da Segunda lei de Newton ou Princípio Fundamental da Dinâmica.
A segunda Lei de Newton ou princípio fundamental da dinâmica diz que, a força aplicada a um objeto é igual à massa do objeto multiplicado por sua aceleração.
A 2º lei de Newton também foi estudada por Galileu e pode ser escrita matematicamente da seguinte forma:
F=m.a
Onde:
F é a força aplicada;
m é a massa do corpo;
a é a aceleração do corpo;
Não é difícil de entender se você pensar no seguinte exemplo, se tivermos dois veículos em uma mesma rua plana, o primeiro veículo é um fusca e o segunda um grande caminhão. A grande diferença entre estes dois veículos é a massa, o caminhão é muito mais pesado que o fusca. Sendo assim, para fazer o caminhão se movimentar, ou seja, para aumentar sua velocidade é necessária uma força muito maior que a força necessária para movimentar o fusca. Se você empurrar o fusca com as próprias mãos, poderá até mesmo movê-lo com certa facilidade, mas dificilmente, conseguirá mover o caminhão desta mesma maneira. A força necessária para acelerar um corpo é diretamente proporcional a sua massa, está é a grande “sacada” da segunda lei de Newton.
A segunda lei é considerada por muitos professores como a mais importante da Mecânica e podemos utilizá-la para analisar movimentos de objetos próximos a Terra e também de corpos celestes. Em muitos exercícios de vestibulares vamos utilizar esta lei para chegar ao resultado esperado.

Segunda Lei de Newton
A segunda lei de Newton, também conhecida como o princípio fundamental da dinâmica, faz uma relação da resultante das forças aplicadas em um corpo com a aceleração exercida por ele.
Para compreender como é feita essa relação considere um corpo qualquer e as resultantes das forças exercidas sobre ele . Essa força resultante vai fazer com que esse corpo sofra uma aceleração , ou seja, irá sofrer uma alteração na sua velocidade.
orientada para baixo a aceleração terá a mesma orientação, veja figura abaixo:
Se aumentarmos gradativamente a intensidade da força
F1 = F2 = F3 = m
a1 a2 a3
m é a massa inercial da partícula e pode, de uma forma geral, demonstrar:
F = m →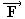 = m .
= m . 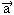
a
No SI, a unidade de medida da força é Newton (N) e a unidade de medida da massa é kg e a unidade de medida da aceleração é s2.
Portanto, a segunda lei de Newton assume o seguinte enunciado:
Se uma partícula sofre uma força resultante F, com relação a essa força a partícula irá adquirir uma aceleração a, onde essa força e essa aceleração irão possuir a mesma direção e mesmo sentido, cujo módulo é diretamente proporcional à intensidade da força
Força de Atrito
Até agora, para calcularmos a força, ou aceleração de um corpo, consideramos que as superfícies por onde este se deslocava, não exercia nenhuma força contra o movimento, ou seja, quando aplicada uma força, este se deslocaria sem parar.
Mas sabemos que este é um caso idealizado. Por mais lisa que uma superfície seja, ela nunca será totalmente livre de atrito.
Sempre que aplicarmos uma força a um corpo, sobre uma superfície, este acabará parando.
É isto que caracteriza a força de atrito:
- Se opõe ao movimento;
- Depende da natureza e da rugosidade da superfície (coeficiente de atrito);
- É proporcional à força normal de cada corpo;
- Transforma a energia cinética do corpo em outro tipo de energia que é liberada ao meio.
A força de atrito é calculada pela seguinte relação:
Segunda Lei de Newton
A segunda Lei de Newton ou princípio fundamental da dinâmica diz que, a força aplicada a um objeto é igual à massa do objeto multiplicado por sua aceleração.
www.efeitojoule.com/2011/.../segunda-lei-de-newton-segunda-lei.html
Daniel Morozeski
Plano Inclinado
Plano Inclinado
Como o próprio nome diz, é um corpo em uma inclinação.
Aceleração no plano inclinado sem atrito
Quando um corpo se move livremente em um plano inclinado, sem atrito, a força resultante é responsável por sua aceleração é a componente tangencia de seu peso:
Aceleração no plano inclinado com atrito
Quando um corpo se move livremente em um plano inclinado, com atrito, a força resultante, responsável pela sua aceleração, é a soma vetorial da componente tangencial de seu peso (Pt) com a força de atrito dinâmica.
2° Lei de Newton:
Ângulo de Atrito
Se o corpo permanecer em repouso no plano inclinado, porém estiver quase para deslizar, isto é, a força de atrito solicitada ao máximo, teremos:
Aceleração no plano inclinado sem atrito
Quando um corpo se move livremente em um plano inclinado, sem atrito, a força resultante é responsável por sua aceleração é a componente tangencia de seu peso:
Aceleração no plano inclinado com atrito
Quando um corpo se move livremente em um plano inclinado, com atrito, a força resultante, responsável pela sua aceleração, é a soma vetorial da componente tangencial de seu peso (Pt) com a força de atrito dinâmica.
2° Lei de Newton:
Ângulo de Atrito
Se o corpo permanecer em repouso no plano inclinado, porém estiver quase para deslizar, isto é, a força de atrito solicitada ao máximo, teremos:
Pedro Bertuani e Eduardo Salles
Força Elastica
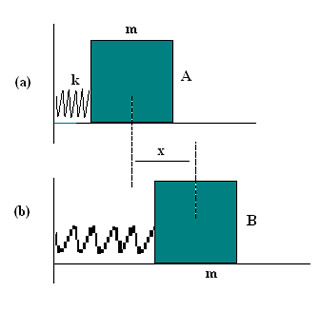
Segundo a lei de Hooke, uma mola, sofrendo uma elongação que aumente ou diminua o seu comprimento de equilíbrio, tende a voltar ao seu comprimento original exercendo uma força de intensidade proporcional à deformação:
F = - kx (k = constante)
onde x mede a elongação a partir do comprimento de equilíbrio e k, a dureza da mola.
O sinal negativo indica que a força tem sentido contrário ao da elongação.
Força elástica
Força elástica
Quando um corpo elástico (por exemplo, uma mola) sofre uma deformação (x) sob a ação de uma força

existe uma relação entre a força e a deformação que obedece à fórmula:

onde k é a constante elástica do corpo elástico, medida em

no sistema internacional de medidas.
A constante é uma característica do corpo, dependendo do material, dimensões etc.

Obs.: a deformação (x) é medida a partir do ponto de repouso da mola.
Força de tração
 A força de tração
A força de traçãoForças de tração são assim denominadas quando forças são exercidas nos corpos por meio de fios. Geralmente consideram-se as cordas e os fios como ideais.
Podemos medir a tração em qualquer ponto de uma corda, colocando ali um dinamômetro. O dinamômetro é um aparelho para medir força.
Outra maneira de medir a força de tração de um objeto ou corpo é igualando a tração com o peso. Vejamos a figura acima, como o corpo está pendurado por uma corda atua sobre ele somente a força de tração e a força peso. De acordo com a segunda Lei de Newton temos:
FR=m.a
Como o corpo se encontra equilibrado, a aceleração é zero.
FR=0
T-P=0 ⇒ T=P ⇒ T=m.g
Assim, concluímos que a tração, nesse caso, é o próprio peso do corpoA força de tração
Forças de tração são assim denominadas quando forças são exercidas nos corpos por meio de fios. Geralmente consideram-se as cordas e os fios como ideais.
Podemos medir a tração em qualquer ponto de uma corda, colocando ali um dinamômetro. O dinamômetro é um aparelho para medir força.
Outra maneira de medir a força de tração de um objeto ou corpo é igualando a tração com o peso. Vejamos a figura acima, como o corpo está pendurado por uma corda atua sobre ele somente a força de tração e a força peso. De acordo com a segunda Lei de Newton temos:
FR=m.a
Como o corpo se encontra equilibrado, a aceleração é zero.
FR=0
T-P=0 ⇒ T=P ⇒ T=m.g
Assim, concluímos que a tração, nesse caso, é o próprio peso do corpo
Elevadores
<iframe width="420" height="315" src="http://www.youtube.com/embed/96offkeDS4c" frameborder="0" allowfullscreen></iframe>
Segunda lei de Newton
A segunda lei de Newton, também chamada de princípio fundamental da dinâmica, afirma que a força resultante em uma partícula é igual a razão do tempo de mudança do seu momento linear  em um sistema de referência inercial:
em um sistema de referência inercial:
 em um sistema de referência inercial:
em um sistema de referência inercial:Segunda Lei de Newton
Também chamada de Princípio Fundamental da Dinâmica, esta lei, a segunda de três, foi estabelecida por Sir Isaac Newton ao estudar a causa dos movimentos. Esse princípio consiste na afirmação de que um corpo em repouso necessita da aplicação de uma força para que possa se movimentar, e para que um corpo em movimento pare é necessária a aplicação de uma força. Um corpo adquire velocidade e sentido de acordo com a intensidade da aplicação da força. Ou seja, quanto maior for a força maior será a aceleração adquirida pelo corpo.
*Aceleração: é a taxa de variação da velocidade. No SI sua unidade é o metro por segundo ao quadrado (m/s2).
Newton estabeleceu esta lei para análise das causas dos movimentos, relacionando as forças que atuam sobre um corpo de massa m constante e a aceleração adquirida pelo mesmo devido à atuação das forças. Esta lei diz que:
A resultante das forças aplicadas sobre um ponto material é igual ao produto da sua massa pela aceleração adquirida:

Esta é uma igualdade vetorial na qual força e aceleração são grandezas vetoriais, as quais possuem módulo, direção e sentido. Esta equação significa que a força resultante (soma das forças que atuam sobre um determinado ponto material) produz uma aceleração com mesma direção e sentido da força resultante e suas intensidades são proporcionais.
*Ponto material: em mecânica esse é um termo utilizado para representar qualquer objeto em virtude do fenômeno, sem levar em consideração suas dimensões. Ou seja, as dimensões não afetam no resultado do fenômeno estudado.
No Sistema Internacional de Unidades (SI), a unidade de força é o newton (N) em homenagem a Newton. Porém, existem outras unidades de medida como o dina e o kgf.
Peso
Peso é a força gravitacional sofrida por um corpo nas vizinhanças de um planeta. É uma grandeza vetorial e, portanto, possui módulo, direção e sentido. Matematicamente temos:
P =m.g
Onde g é a aceleração da gravidade local.
A massa de um corpo não muda. O que muda é seu peso em razão da ação da força gravitacional, que pode ser maior ou menor, dependendo da localização do corpo.
Giovana Monnerat e Laila Alves
Também chamada de Princípio Fundamental da Dinâmica, esta lei, a segunda de três, foi estabelecida por Sir Isaac Newton ao estudar a causa dos movimentos. Esse princípio consiste na afirmação de que um corpo em repouso necessita da aplicação de uma força para que possa se movimentar, e para que um corpo em movimento pare é necessária a aplicação de uma força. Um corpo adquire velocidade e sentido de acordo com a intensidade da aplicação da força. Ou seja, quanto maior for a força maior será a aceleração adquirida pelo corpo.
*Aceleração: é a taxa de variação da velocidade. No SI sua unidade é o metro por segundo ao quadrado (m/s2).
Newton estabeleceu esta lei para análise das causas dos movimentos, relacionando as forças que atuam sobre um corpo de massa m constante e a aceleração adquirida pelo mesmo devido à atuação das forças. Esta lei diz que:
A resultante das forças aplicadas sobre um ponto material é igual ao produto da sua massa pela aceleração adquirida:
Esta é uma igualdade vetorial na qual força e aceleração são grandezas vetoriais, as quais possuem módulo, direção e sentido. Esta equação significa que a força resultante (soma das forças que atuam sobre um determinado ponto material) produz uma aceleração com mesma direção e sentido da força resultante e suas intensidades são proporcionais.
*Ponto material: em mecânica esse é um termo utilizado para representar qualquer objeto em virtude do fenômeno, sem levar em consideração suas dimensões. Ou seja, as dimensões não afetam no resultado do fenômeno estudado.
No Sistema Internacional de Unidades (SI), a unidade de força é o newton (N) em homenagem a Newton. Porém, existem outras unidades de medida como o dina e o kgf.
Peso
Peso é a força gravitacional sofrida por um corpo nas vizinhanças de um planeta. É uma grandeza vetorial e, portanto, possui módulo, direção e sentido. Matematicamente temos:
P =m.g
Onde g é a aceleração da gravidade local.
A massa de um corpo não muda. O que muda é seu peso em razão da ação da força gravitacional, que pode ser maior ou menor, dependendo da localização do corpo.
Giovana Monnerat e Laila Alves
Força de Tração
Em muitas situações do cotidiano, em função da praticidade, é conveniente utilizarmos cabos e cordas para transmitirmos forças a um corpo.
Por exemplo, quando vamos pescar utilizamos uma vara com um fio de nylon para fisgar o peixe. Ninguém em sã consciência pensaria em pegar peixe na "unha" ! |  |
Quando desejamos rebocar um carro utilizamos uma corda. O mesmo ocorre quando desejamos “puxar” água de um poço, fazer com que um elevador suba ou desça, soltar pipa ou elevar uma ponte móvel.
| |||
Força Elástica

Imagine uma mola presa em uma das extremidades a um suporte, e em estado de repouso (sem ação de nenhuma força).
Quando aplicamos uma força F na outra extremidade, a mola tende a deformar (esticar ou comprimir, dependendo do sentido da força aplicada).
Ao estudar as deformações de molas e as forças aplicadas, Robert Hooke (1635-1703), verificou que a deformação da mola aumenta proporcionalmente à força. Daí estabeleceu-se a seguinte lei, chamada Lei de Hooke:
Onde:
F: intensidade da força aplicada (N);
k: constante elástica da mola (N/m);
x: deformação da mola (m).
A constante elástica da mola depende principalmente da natureza do material de fabricação da mola e de suas dimensões. Sua unidade mais usual é o N/m (newton por metro) mas também encontramos N/cm; kgf/m, etc.
Giovana Monnerat e Laila Alves.
Giovana Monnerat e Laila Alves.
Assinar:
Comentários (Atom)




